
February 4, 2025
4 min read
Mathematicians Solve Infamous ‘Moving Sofa Problem’
What’s the largest couch that can turn a corner? After 58 years, we finally know

For those who have wrestled a bulky couch around a tight corner and lamented, “Will this even fit?” mathematicians have heard your pleas. Geometry’s “moving sofa problem” asks for the largest shape that can turn a right angle in a narrow corridor without getting stuck. The problem sat unsolved for nearly 60 years until November, when Jineon Baek, a postdoc at Yonsei University in Seoul, posted a paper online claiming to resolve it. Baek’s proof has yet to undergo thorough peer review, but initial passes from mathematicians who know Baek and the moving sofa problem seem optimistic. Only time will tell why it took Baek 119 pages to write what Ross Geller of the sitcom Friends said in one word.
The solution is unlikely to help you on moving day, but as frontier math grows more abstruse, mathematicians hold a special fondness for unsolved problems that anybody can understand. In fact, the popular math forum MathOverflow maintains a list of “Not especially famous, long-open problems which anyone can understand,” and the moving sofa problem currently ranks second on the list. Still, every proof expands our understanding, and the techniques used to resolve the moving sofa problem will likely lend themselves to other geometric puzzles down the road.
The rules of the problem, which Canadian mathematician Leo Moser first formally posed in 1966, involve a rigid shape—so the cushions don’t yield when pressed—turning a right angle in a hallway. The sofa can be any geometric shape; it doesn’t have to resemble a real couch. Both the shape and the hallway are two-dimensional. Imagine the sofa weighs too much to lift, and you can only slide it.
On supporting science journalism
If you’re enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
A quick tour through the problem’s history reveals the extensive effort that mathematicians have poured into it—they were no couch potatoes. Faced with an empty hallway, what is the largest shape you could squeeze through it? If each leg of the corridor measures one unit across (the specific unit doesn’t matter), then we can easily scoot a one-by-one square through the passage. Elongating the square to form a rectangle fails instantly, because once it hits the kink in the hallway, it has no room to turn.
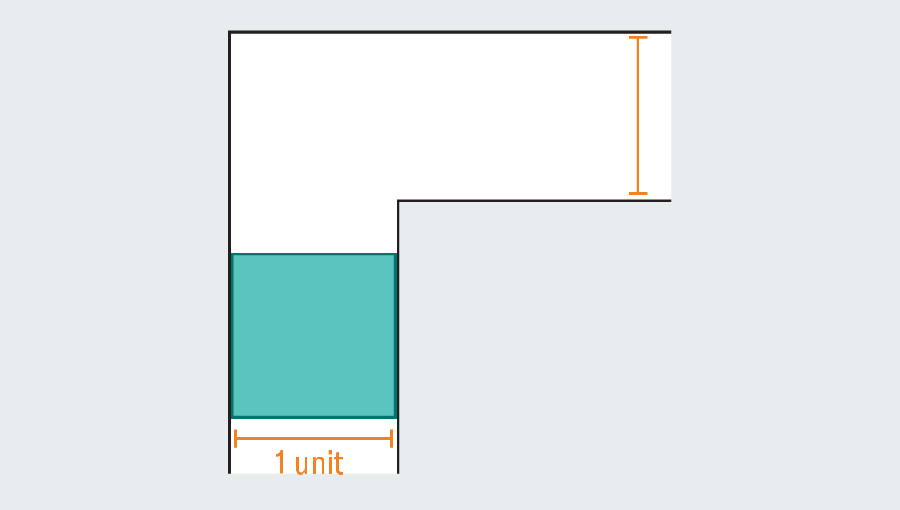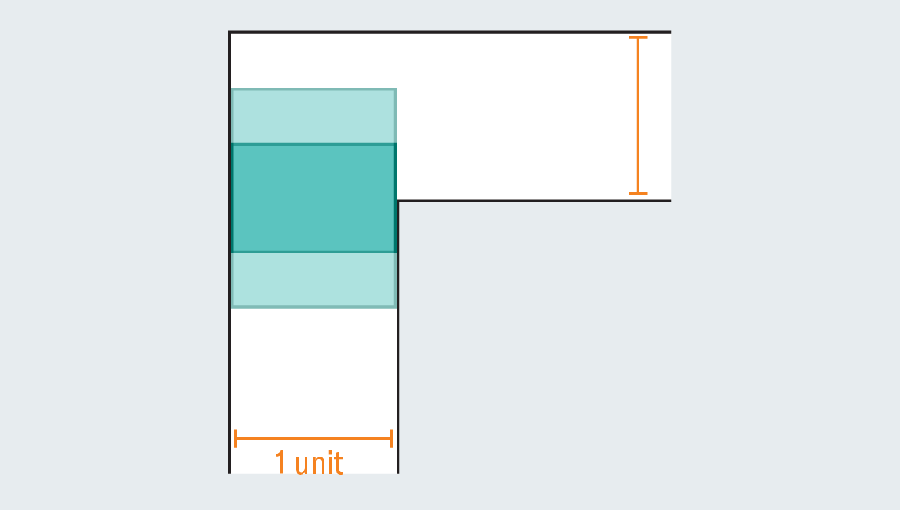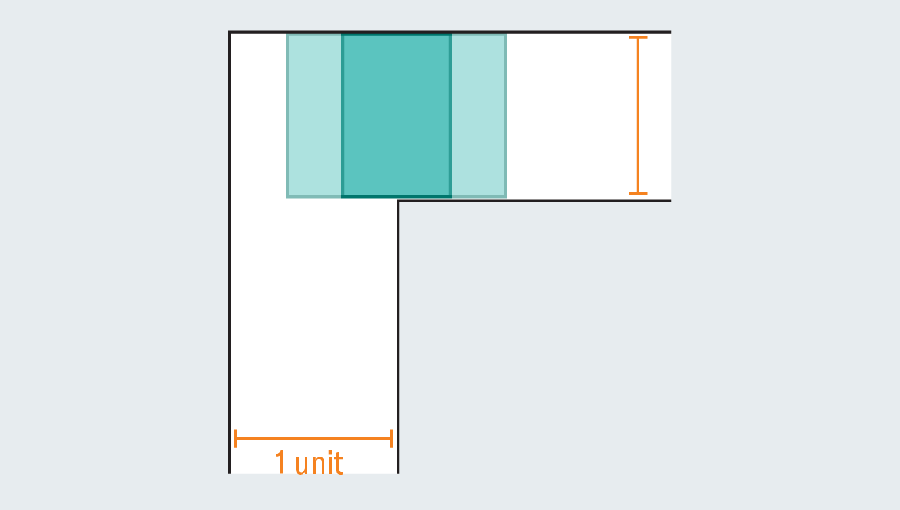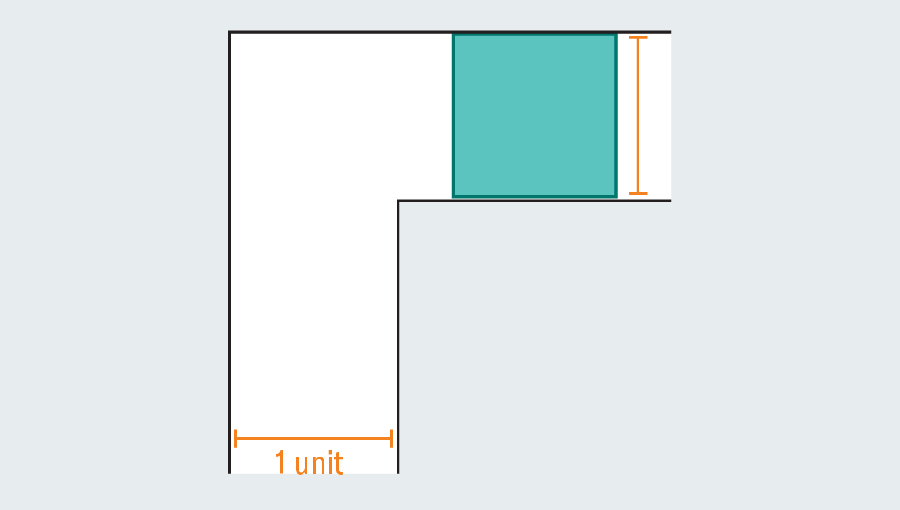
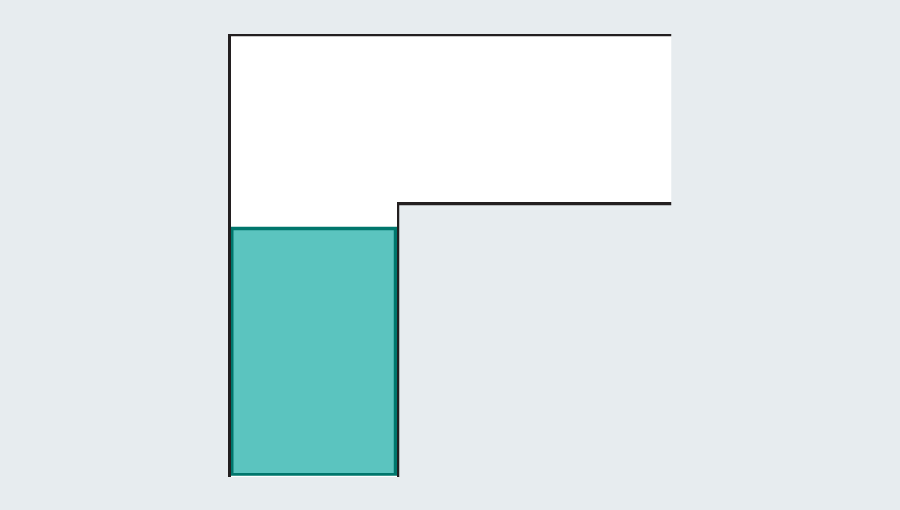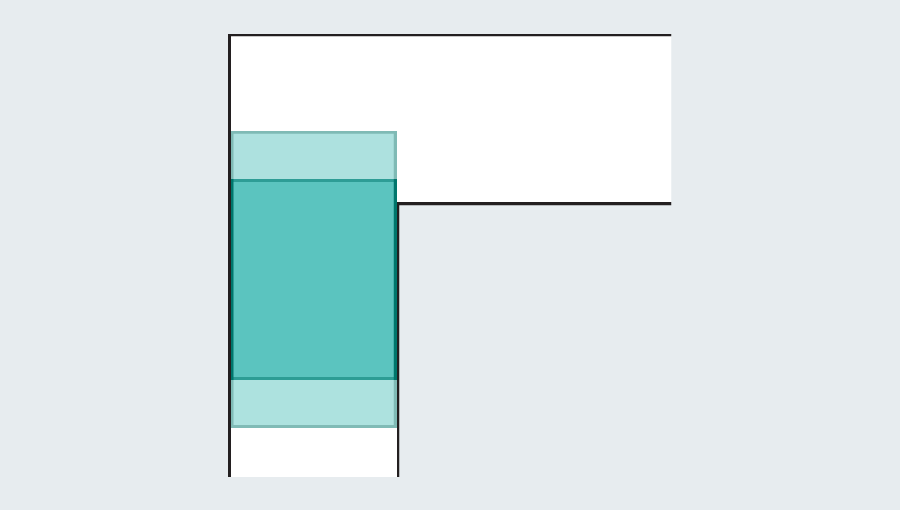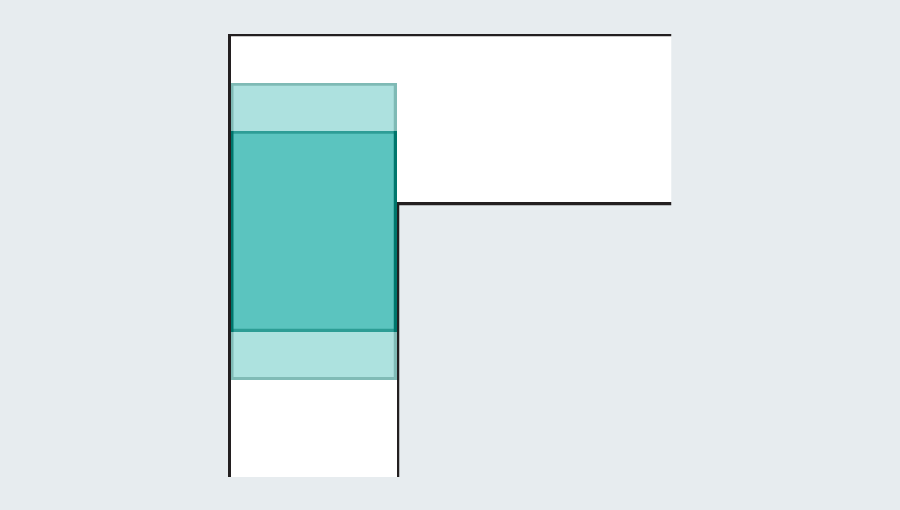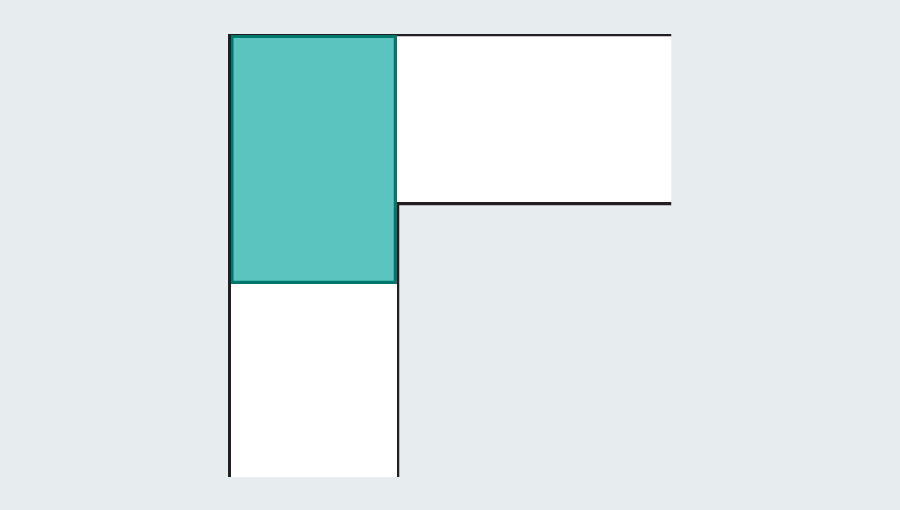
Yet mathematicians realized they can go bigger by introducing curved shapes. Consider a semicircle with a diameter (the straight base) of 2. When it hits the turn, much of it still overhangs in the first leg of the hallway, but the rounded edge leaves just enough room to clear the corner.
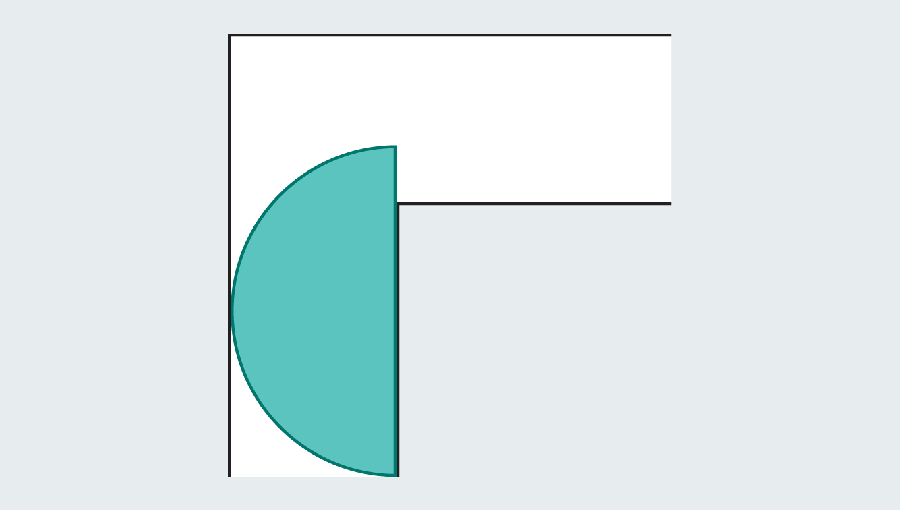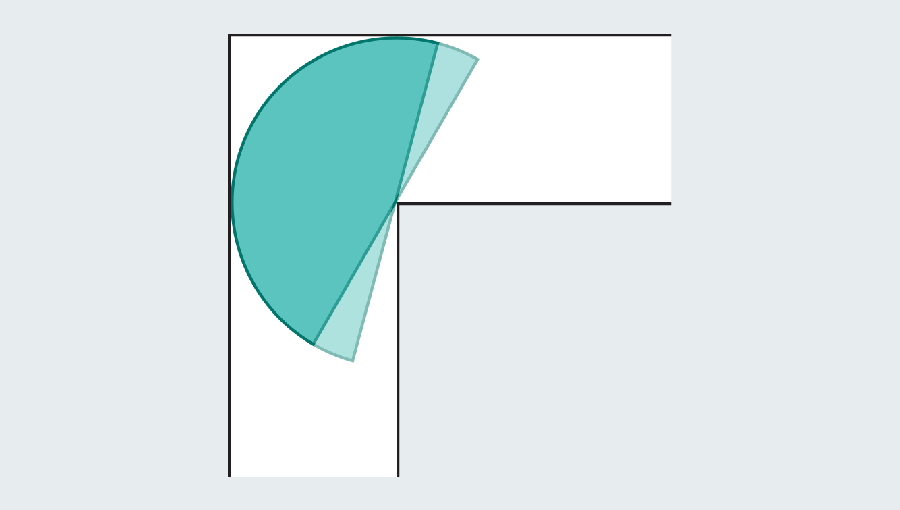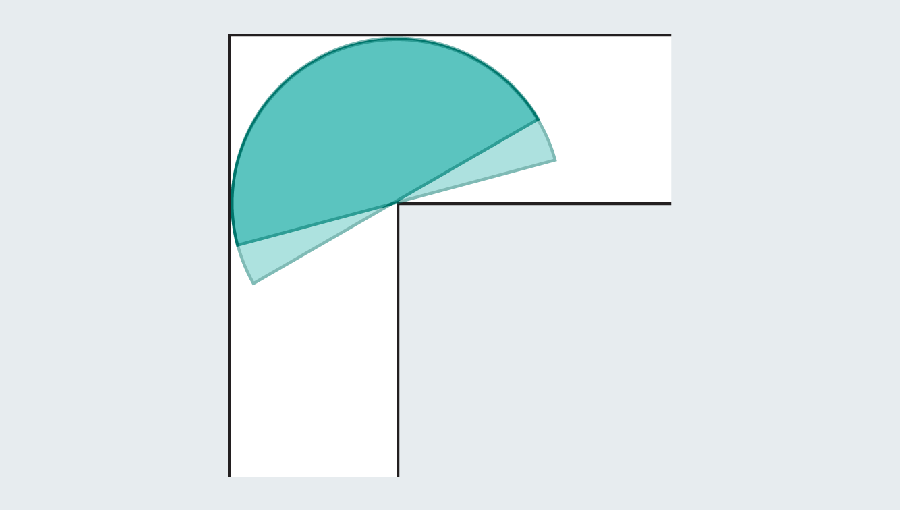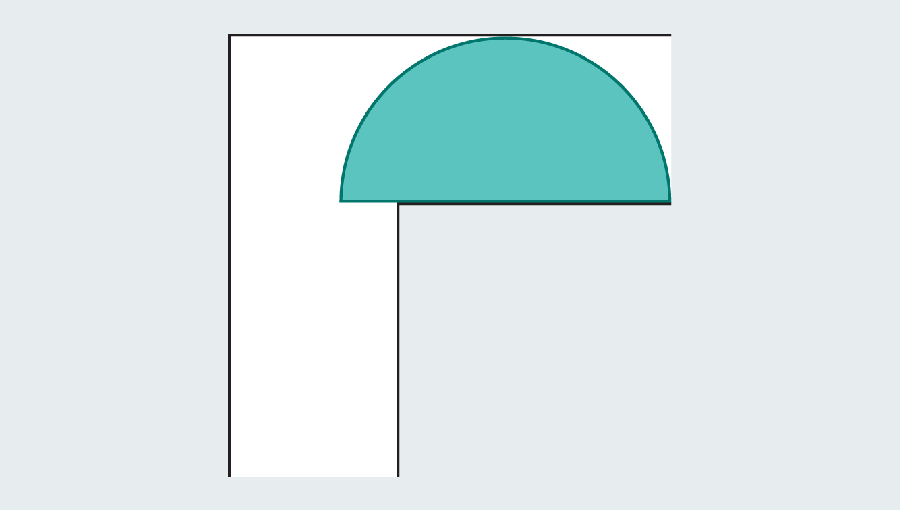
Remember the goal is to find the largest “couch” that slides around the corner. Dusting off our high school geometry formulas, we can calculate the area of the semicircle as π/2, or approximately 1.571. The semicircle gives a significant improvement over the square, which had an area of only 1. Unfortunately both would look strange in a living room.
Solving the moving sofa problem requires that you not only optimize the size of a shape, but also the path that shape traverses. The setup permits two types of motion: sliding and rotating. The square couch only slid, whereas the semicircle slid, then rotated around the bend, and then slid again on the other side. But objects can slide and rotate at the same time. Mathematician Dan Romik of the University of California, Davis, has noted that a solution to the problem should optimize both types of motion simultaneously.
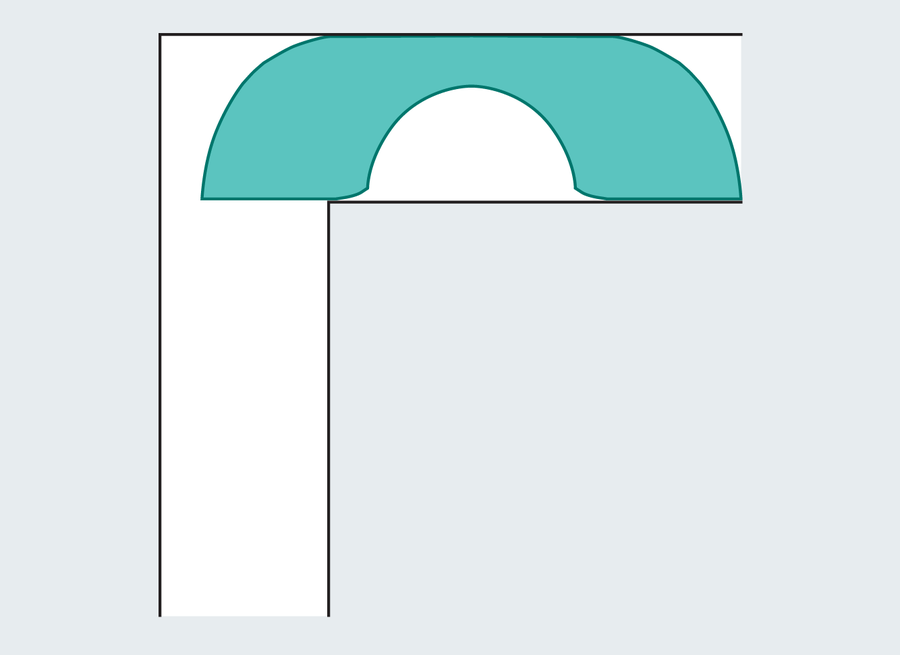
British mathematician John Hammersley discovered in 1968 that stretching the semicircle can buy you a larger sofa if you carve out a chunk to deal with that pesky corner. Furthermore, Hammersley’s sofa takes advantage of a hybrid sliding plus rotating motion. The resulting sofa looks like a landline telephone:

Amanda Montañez; Source: “On Moving a Sofa Around a Corner,” by Joseph L. Gerver, in Geometriae Dedicata, Vol. 42, No. 3; June 1992 (reference)
Optimizing the different variables yields a sofa with area π/2 + 2/π, or approximately 2.2074. This is a huge upgrade from the semicircle, akin to moving from a love seat to a sectional. But progress stalled there for 24 years. The next significant improvement would be the last. In 1992 Joseph Gerver unveiled a masterwork of mathematical carpentry, which we now know to be the largest possible sofa.
Amanda Montañez; Source: “On Moving a Sofa Around a Corner,” by Joseph L. Gerver, in Geometriae Dedicata, Vol. 42, No. 3; June 1992 (reference)
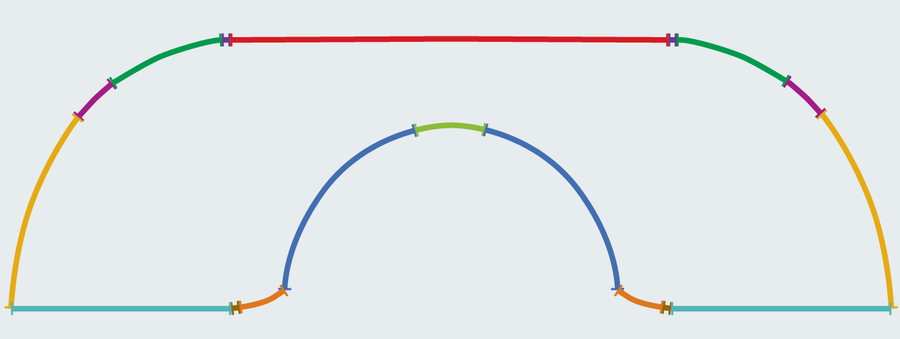
You’d be forgiven for feeling déjà vu right now. Gerver’s sofa looks identical to Hammersley’s, but it’s a much more complicated construction. Gerver stitched together 18 distinct curves to form his shape. On closer inspection you might spot some differences, especially the beveled edges at the base of the rounded cutout.
Amanda Montañez; Source: “On Moving a Sofa Around a Corner,” by Joseph L. Gerver, in Geometriae Dedicata, Vol. 42, No. 3; June 1992 (reference)
The area of Gerver’s triumph measures in at 2.2195 units. Surprisingly, Hammersley’s relatively simple sofa only fell about .012 short of optimal. Although only a skosh larger than its predecessor, Gerver suspected that his discovery reached the maximum possible size. He couldn’t prove it though. And neither could anybody else for another 32 years.
Baek finished his Ph.D. in 2024 and wrote his thesis on the moving sofa problem, contributing several incremental insights. That same year, he sewed all of his fresh ideas together into an impressive opus that proves no sofa larger than Gerver’s can squeeze through the hallway. Cracking a long-standing open problem is a dream for any mathematician, let alone one so early in their career. If Baek’s work withstands scrutiny, he will likely find himself in high demand for professorships. Unless he pivots into furniture making.
Source link




